

Next: About this document ...
Up: Detecting Format String Vulnerabilities
Previous: Bibliography
Theorem A.1
Let
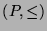
be any finite partial order. Let
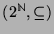
be the lattice of subsets of
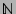
with the set
inclusion ordering. Then there exists a mapping
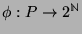
, such that
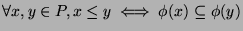
and
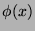
is a finite subset of
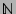
for all
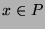
.
Proof :
We prove the theorem by induction on 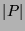 .
.
Base Case : Let 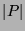 = 1. Then the claim trivially holds.
= 1. Then the claim trivially holds.
Induction Hypothesis : Let the
claim hold for all 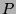 such that
such that
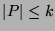 .
.
Induction Step : 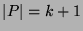 .
.
Let 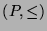 be a partial order such that
be a partial order such that 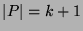 . Since
. Since 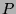 is finite,
is finite, 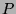 has a minimal element, say
has a minimal element, say
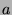 . Consider the partial order
. Consider the partial order
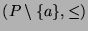 . Clearly
this is a partial order and
. Clearly
this is a partial order and
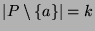 . Hence by
induction hypothesis, there exists
. Hence by
induction hypothesis, there exists
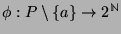 , such that
, such that
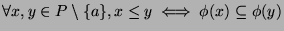 and
and 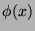 is a
finite subset of
is a
finite subset of
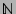 for all
for all
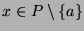 . Let
. Let
 . Define
. Define
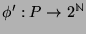 as follows.
as follows.
Since 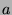 was chosen to be a minimal element, the only relations
involving
was chosen to be a minimal element, the only relations
involving 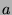 are of the form
are of the form 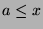 , and for these, by
definition,
, and for these, by
definition,
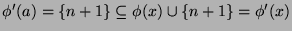 . For all
. For all 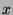 such that
such that
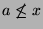 , we have
, we have
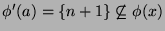 by choice of
by choice of 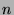 . For relations not
involving
. For relations not
involving 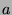 , the show below that the set containment relations are
preserved. Let
, the show below that the set containment relations are
preserved. Let
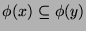 . Since
. Since
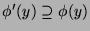 , the case when
, the case when
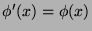 is trivial. So
assume
is trivial. So
assume
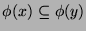 and
and
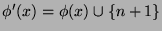 . This
implies that
. This
implies that 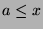 , and
, and 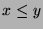 , and therefore
, and therefore 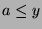 . Thus
. Thus 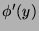 would be defined as
would be defined as
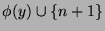 , and hence
, and hence
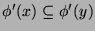 .Thus the induction
step holds.
.Thus the induction
step holds.


Next: About this document ...
Up: Detecting Format String Vulnerabilities
Previous: Bibliography
Umesh Shankar
2001-05-16
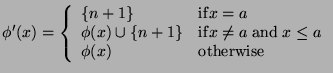
![]() was chosen to be a minimal element, the only relations
involving
was chosen to be a minimal element, the only relations
involving ![]() are of the form
are of the form ![]() , and for these, by
definition,
, and for these, by
definition,
![]() . For all
. For all ![]() such that
such that
![]() , we have
, we have
![]() by choice of
by choice of ![]() . For relations not
involving
. For relations not
involving ![]() , the show below that the set containment relations are
preserved. Let
, the show below that the set containment relations are
preserved. Let
![]() . Since
. Since
![]() , the case when
, the case when
![]() is trivial. So
assume
is trivial. So
assume
![]() and
and
![]() . This
implies that
. This
implies that ![]() , and
, and ![]() , and therefore
, and therefore ![]() . Thus
. Thus ![]() would be defined as
would be defined as
![]() , and hence
, and hence
![]() .Thus the induction
step holds.
.Thus the induction
step holds.